高校の理科科目である、物理や化学、生物、地学の計算で苦労するのが有効数字の考え方です。慣れれば苦にすることはないのですが、最初がどうしても難しく感じてしまうはずです。今日は、高校理科の計算で必要な有効数字の考え方をレクチャーします。
有効数字とは?
理科で取り扱う数値は、実験で得られた測定値になります。測定値や測定値を使った計算で得られた値には末位に誤差を含んでいます。
例えば、中学生の時に学習したメスシリンダーや温度計の読み取り方で、最小の目盛りの10分の1まで目盛りを読むと学習しましたね。下のメスシリンダーの液量は、最小の目盛りの10分の1まで読むと5.3mLになります。
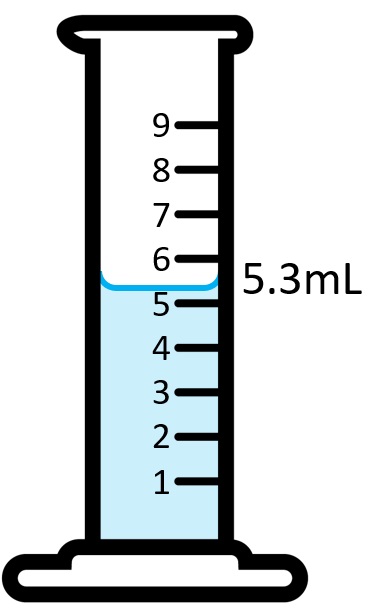
目分量で読み取っているのですから、誤差を含む数値です。実際は四捨五入して5.3mLになる数値5.25以上5.35未満のどれかの数値が真の値となります。
液面が5と6の間にあるので、1の位の5mLということは疑う余地はありません。小数第1位の0.3mLという数値は見る人によっては0.4mLや0.2mLと読むかもしれませんので、不確かさが残る数値です。小数第2位はこのメスシリンダーでは測定できません。
したがって、この液量は5.3mLで、小数第1位は不確かさを含んでいるので、5.25mL以上5.35mL未満の幅がある数字だといえます。このように、誤差を含みながらも、測定値として意味をもつ桁だけを表示したものが有効数字になるのです。
有効数字の数え方
有効数字は、大きい位に0以外の数字が登場してから末位までの数字の並んでいる個数になります。
- 10…有効数字2桁
- 100…有効数字3桁
- 1.0…有効数字2桁
- 1.00…有効数字3桁
- 0.1…有効数字1桁
- 0.01…有効数字1桁
- 0.010…有効数字2桁
0.1や0.01の0は位取りのゼロですので有効数字の桁数に入れません。数字のあとに登場するゼロは意味があるので有効数字の桁数に含めます。
- 0.1…0.05以上0.15未満
- 0.10…0.095以上0.105未満
このように、示している数字の幅が異なります。
5.6gと5600mgは違う
1g=1000mgなので、5.6g=5600mgになりますが、測定値の場合5.6gと5600mgは異なります。5.6gと5600mgの測定値の幅を見てみると、
- 5.6g…5.55g以上5.65g未満
- 5600mg…5599.5mg以上5600.5mg未満(5.5995g以上5.6005g未満)
このように測定値では数値の幅が異なりますので、有効数字をそろえて意味を同じにする必要があります。
5600mg=5.6×10³mg
こうすれば、5.6gと5.6×10³mgは同じ幅の数値を表すことになるのです。
数値の桁がわかりやすいように○.○で表示
有効数字で数字を表すとき、何で○.○×10ⁿで表記するのでしょう。それは、数字を見ただけで桁数がわかりやすいようにするためです。
例えば1000000という数字がある場合、パッと見ただけでは100万だとわかりづらいですよね。これを1.0×10⁶とすれば、1以下に0が6個並んでいる数字、つまり100万だとわかりやすくなります。これは10×10⁵や0.1×10⁷だと逆にわかりづらくなりますので、○.○×10ⁿで表記するようにしましょう。
有効数字の加減算
まずは、有効数字の加減算を見ていきましょう。次のような計算があったとします。
49.1+12.51
数値には幅がありましたね。
49.1という数値は、49.05以上49.15未満という幅があり、
12.51という数値には、12.505以上12.515未満という幅があります。
49.1の小数第2位の数字があてにならない数字ですので、12.51の小数第2位もあてにならない数字となってしまいます。したがって、この計算の答えは、
49.1+12.51=61.6
となります。つまり、加減算では最小の位の大きいほうに合わせるように四捨五入することになるのです。上の計算では、49.1が小数第1位、12.51が小数第2位まであるので、答えは小数第1位まで求めることになります。
有効数字の乗除算
次は乗除算の計算方法です。次のような計算があったとします。
12.5×5.641
数値には幅がありましたね。
12.5という数値は、12.45以上12.55未満という幅があり、
5.641という数値には、5.6405以上5.6415未満という幅があります。
計算結果が最も最小になるのは、
12.45×5.6405=70.224225
計算結果が最も最大になるのは、
12.55×5.6415=70.800825
になります。
この場合、12.5の小数第2位の数値はあてにならないので、計算結果の最大と最小の平均70.512525を小数第2位で丸めると70.5となります。
12.5は有効数字3桁、5.641は有効数字4桁で、答えは70.5で有効数字3桁となっています。つまり、乗除算の場合には、有効数字が小さいほうに答えを合わせるように四捨五入するのです。
このように、有効数字を意識して計算することになりますが、実際は問題文に「有効数字3桁で答えよ」などの指示が出されますので、それに従って計算することになります。


コメント