高校生の物理で、まず最初に登場するのが運動の表し方になります。「移動距離」や「速さ」とは若干異なる「変位」や「速度」。さらには「加速度」といった新しい物理量が登場するので、基本をしっかりと押さえていきましょう。
変位とは
変位とは、物体がどの向きにどれだけ移動したかを表す量で、大きさだけでなく向きも関係します。簡単にいうと「位置の変化」が変位になります。変位は、グラフのx座標、y座標を使ってxやyで表します。位置の変化ですので、変化量を意味するΔ(デルタ)を前につ行けて、Δxなどと表します。単位は基本的に[m]を使います。
変位は、物体の経路(通った道)によらず、最初の位置と終わりの位置だけで決まります。変位と似た量として、移動距離がありますが、移動距離の場合は、途中の経路によって量が変わります。また、向きも関係しましせん。
変位Δxは、終わりの位置xから最初の位置x0を引いて求めます。このとき、向きが重要になるので、どちら向きが正の向きになるのかを決めておきましょう。
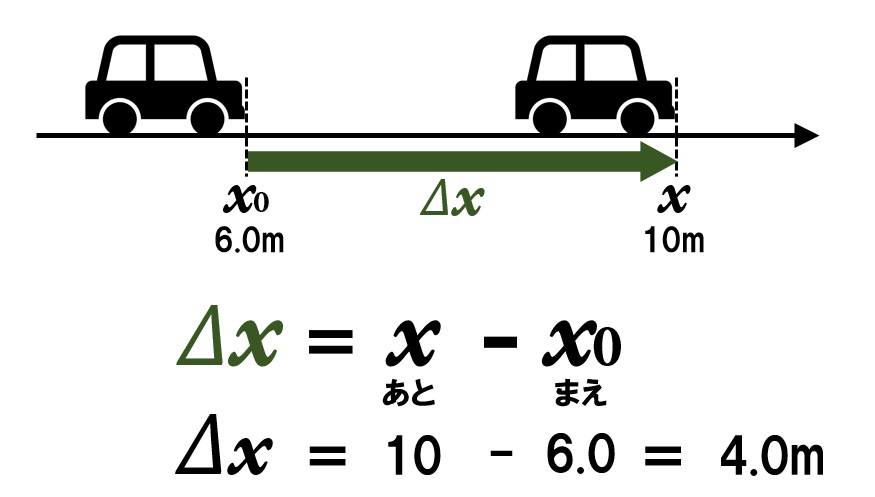
変位の練習問題
次の変位を求めよ。ただし、右向きを正の向きとする。
(1)原点にいた物体が、原点の右12mの位置に移動した。
(2)原点にいた物体が、原点の左8.0mの位置に移動した。
(3)原点の左5.0mの位置にいた物体が、原点の右15mの位置に移動した。
(4)原点の右9.0mの位置にいた物体が、原点の左3.0mの位置に移動した。
(5)原点にいた物体が、原点の右10mの位置に移動し、その後原点の左2.0mの位置に移動した。
変位の練習問題 解答
(1)12m
終わりの位置-最初の位置=変位
+12-0=12
(2)-8.0m
-8.0-0=-8.0
(3)20m
+15-(-5.0)=20
(4)-12m
-3.0-(+9.0)=-12
(5)-2.0m
最初の位置と最後の位置で変位は求まります。
-2.0-0=-2.0
速度とは
速度とは、単位時間(1秒)あたりの物体の変位(位置の変化)です。これまで、計算で使ってきた「速さ」と意味はほぼ同じです。速度は記号v(velocity)であらわし、単位は基本的に[m/s]を使います。
速度と速さは、向き持つ量かどうかの違いがあります。速さの場合、大きさだけで向きを考慮していません。右向きに10m/s、左向きに10m/sの速さで移動しても、どちらも10m/sと表します。しかし、速度の場合は、右向きを正の向きにした場合、右向き10m/sを+10m/s、左向き10m/sは-10m/sと表します。
速度vは、終わりの位置xから最初の位置x0を引いて変位Δxを求め、それを経過時間Δtで割って求めることができます。向きが重要になるので、どちら向きが正の向きになるのかを決めておきましょう。
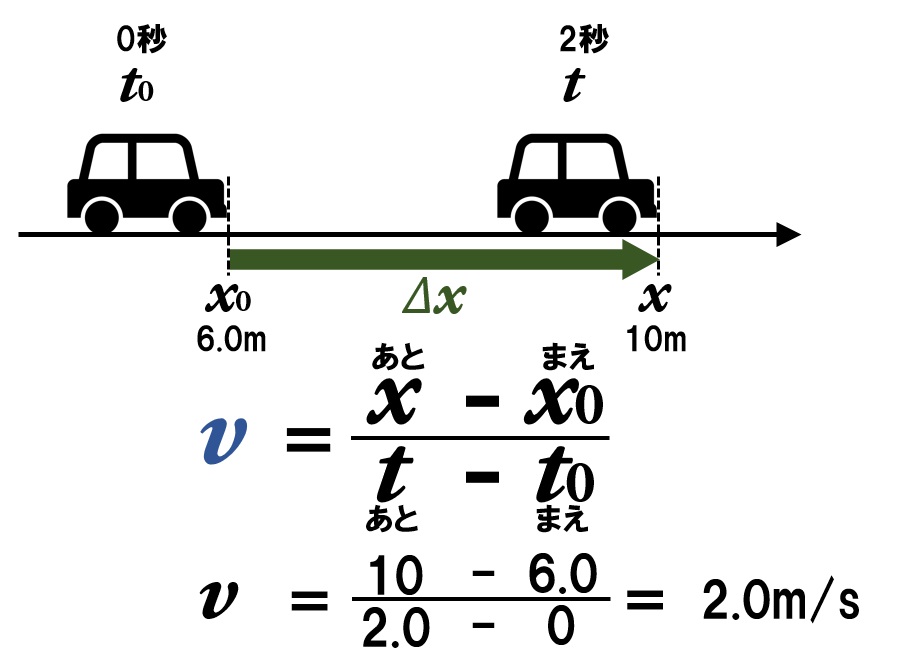
速度には、ある区間を一定の速度で進んだとみなす「平均の速度」と、ごく短い間での変位で求める「瞬間の速度」があります。
速度の練習問題
次の物体の速度を求めよ。ただし、右向きを正の向きとする。
(1)原点にいた物体が、2.0秒間で原点の右12mの地点に移動した。
(2)t=0のとき、原点の右6.0mの位置にいた物体が、t=6.0のとき、原点の左12mの位置にいた。
速度の練習問題 解答
(1)6.0m/s
変位/経過時間で速さを速度は求まります。
12-0 / 2.0=6.0
(2)-3.0m/s
-12-(+6) / 6.0-0 = -3.0
加速度とは
加速度とは、単位時間(1秒)あたりの速度vの変化を加速度といいます。1秒ごとに速度がどれだけ変化しているのかを表している量になります。加速度は記号a(acceleration)で表し、単位は[m/s2](メートル毎秒毎秒)で表します。
加速度aは、最終的な速度vから最初の速度である初速度v0を引き、速度の変化Δvを求め、それを経過時間Δtで割って求めることができます。向きが重要になるので、どちら向きが正の向きになるのかを決めておきましょう。
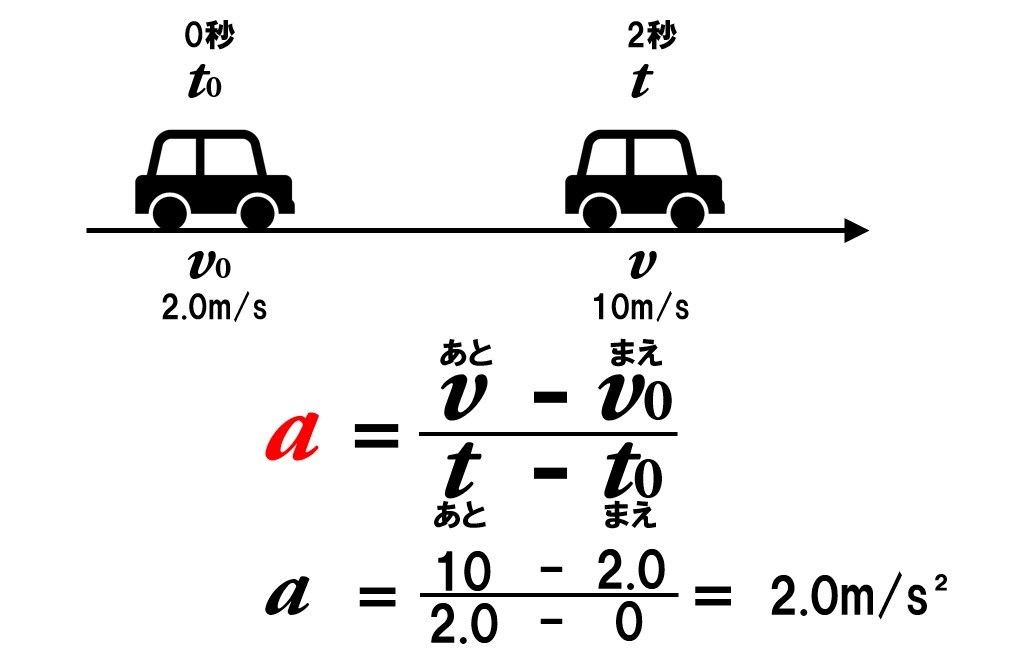
加速度の練習問題
次の場合の加速度を求めよ。ただし、右向きを正の向きとする。
(1)一直線上を右向きに6.0m/sで進む物体が、3.0秒後に右向き12m/sの速さになった。
(2)一直線上を右向きに4.0m/sで進む物体が、4.0秒後に左向き4.0m/sの速さになった。
(3)止まっていた物体が、2.0秒間で右向き6.0m/sの速さになった。
加速度の練習問題 解答
(1)右向き2.0m/s2
速度の変化Δv/経過時間Δtで加速度を求めることができます。
12-6.0 / 3.0 = 2.0
(2)左向き2.0m/s2(-2.0m/s2)
-4.0-(+4.0) / 4.0 = -2.0
(3)右向き3.0m/s2
6.0-0 / 2.0 = 3.0
グラフと変位・速度・加速度
物体の運動では、運動のようすを表すグラフが登場します。x-t図とv-t図です。それぞれのグラフで何を意味しているかを覚えましょう。
x-t図
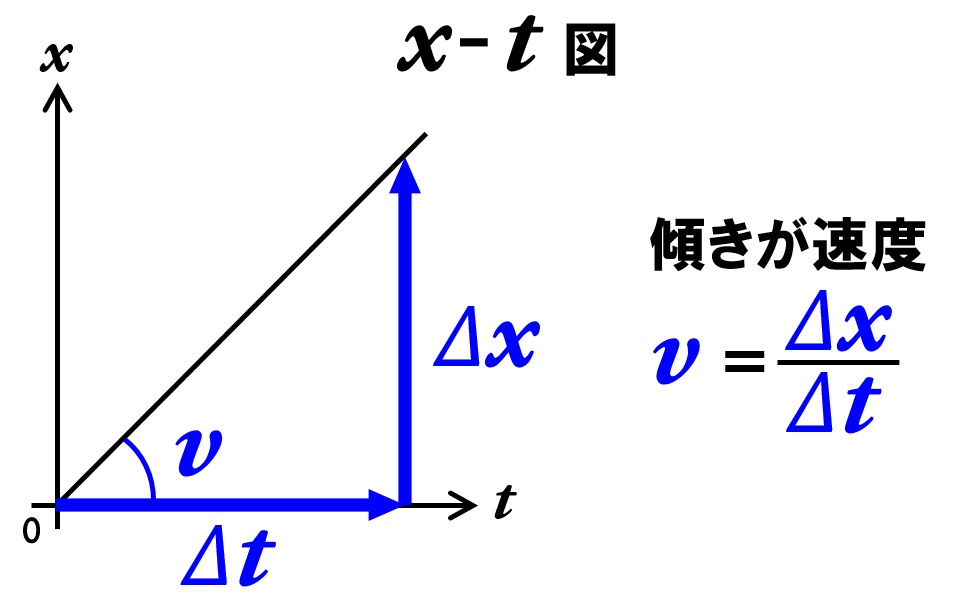
変位(移動距離)xと時間tのグラフです。時間が経過すると、物体の位置がどのように変化するのかを表しています。下のグラフは、時間の経過とともに一定の割合で位置が変化しています。これは、速度が一定で、等速直線運動をしていることを表しています。
x-t図では、グラフの傾きで速度vを表します。傾きが一定ですので、等速直線運動です。
v-t図
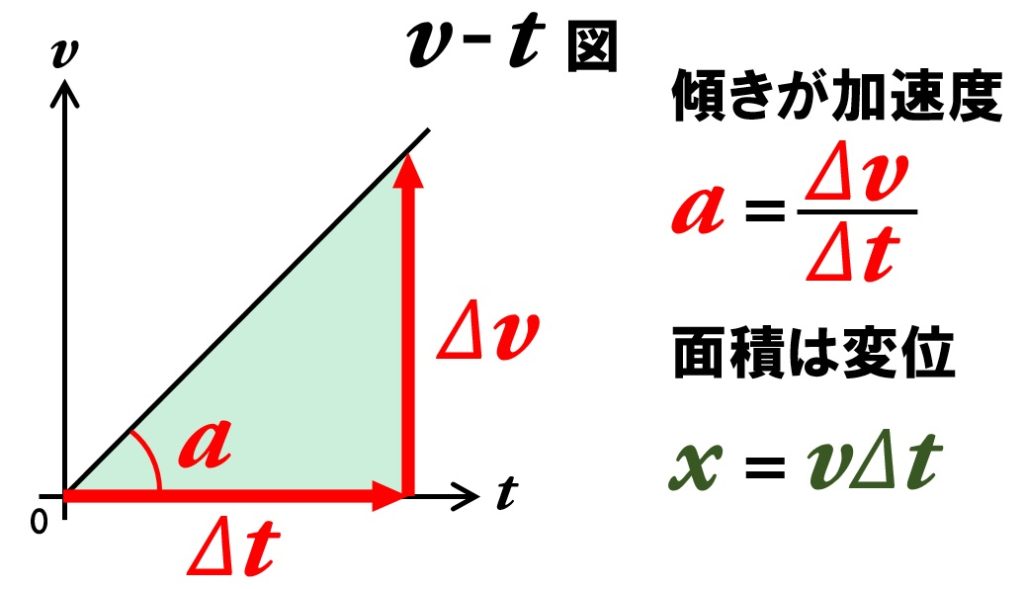
速度vと時間tのグラフです。時間が経過すると、物体の速度がどのように変化するのかを表しています。下のグラフは、時間の経過とともに一定の割合で速度が変化しているので、だんだん速くなる運動(等加速度直線運動)であることがわかります。
v-t図では、グラフの傾きで加速度a、グラフで囲まれた面積で変位(移動距離)xを表します。傾きが一定ですので、等加速度直線運動です。


コメント