【物理基礎】等加速度直線　公式の導出と練習問題

物理基礎の力と運動、等加速度直線運動について学習します。ここでは、等加速度直線運動の3式が登場します。「どの公式を使えばいいのかわからない」という質問が多く出るところです。公式の導出もあわせて学習していきましょう。

等加速度直線運動

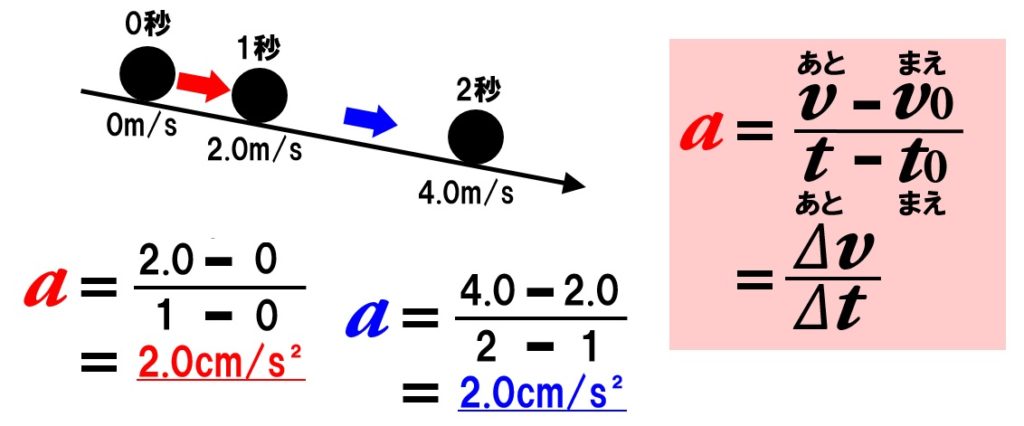
角度が一定の傾きの斜面上を、小球が転がる運動を想像してください。小球は斜面を下るにつれて、だんだんと速くなっていきます。このとき、斜面の角度が一定で変化しませんので、速度の増加する割合は一定になります。

例えば、最初の1秒間で速度が2.0m/s増加したならば、更に1秒時間が経過すると、2.0m/s速度が増加するといった運動です。これが等加速度直線運動です。1秒あたりの速度の増加量が一定ですので、加速度ａが一定になります。

等加速度直線運動の速度の式

等加速度直線運動での速度の求め方ですが、今までのように距離÷時間では速度を求めることができません。なぜなら、加速度ａがあるので、速度が時間の経過とともに変化するからです。

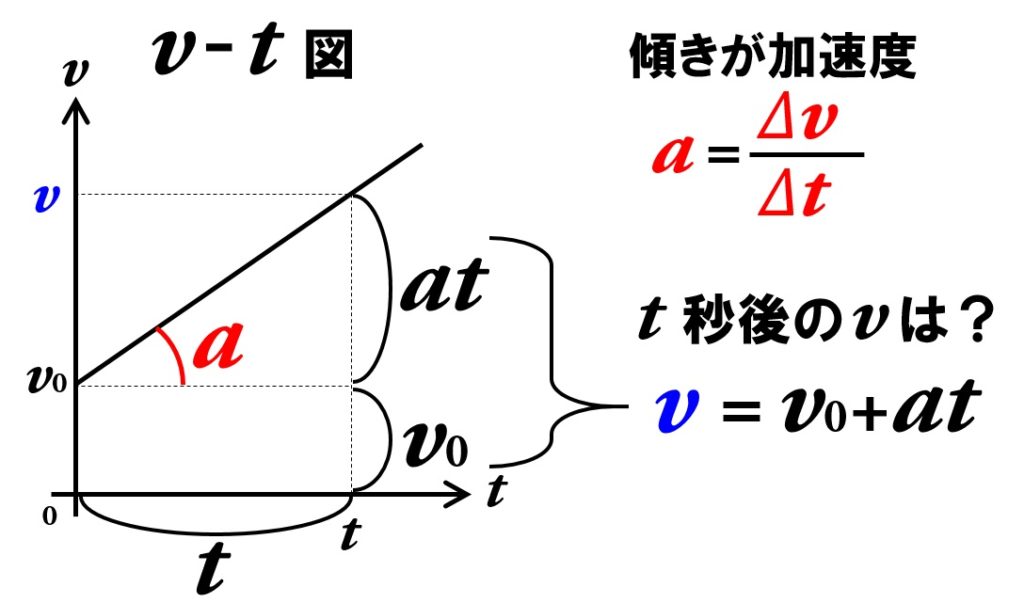
時刻0秒での、物体の速度をv0（初速度）として、等加速度直線運動の速度を求める式を、下のv‐t図から導きます。

等加速度直線運動の変位の式

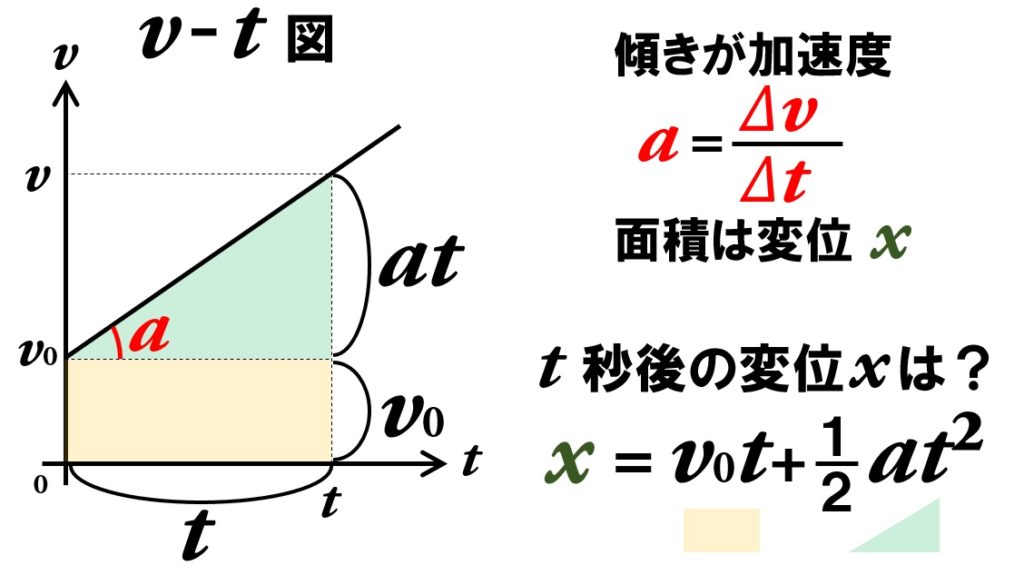
次は、等加速度直線運動の変位（移動距離）を求める式です。v‐t図の面積が変位（移動距離）を表していたことは前回学習しました。変位（移動距離）＝速度×時間ですから、グラフの面積を求めていることと同じでしたね。

では、等加速度直線運動の場合のv‐t図で、変位（移動距離）を考えてみましょう。

等加速度直線運動の時間を消去した式

等加速度直線運動には、３つ目の式として「t（時間）を消去した式」というものが登場します。ここまで求めてきた、速度vの式、変位xの式を連立させtを消去すると、次の式が得られます。なぜこの式が出てくるのか知りたい人は、速度vの式をtについて整理し、変位xの式に代入してみてください。

等加速度直線運動の3式

ここまで出てきた３つの式をまとめてみます。

問題に与えられた条件で使い分けます。３式に登場する文字のうち1つが判明していない状況になっていると思いますので、登場するする数字にどれなのかを考えながら問題文を読んでいくと、自ずと使う公式が変わります。

早速ですが、下の練習問題で慣れていきましょう。

等加速度直線運動の計算　練習問題

次の各問いに答えよ。ただし、初速度（または運動）の向きを正の向きにとし、すべて等加速度直線運動とする。

（1）2.0m/sの速さで運動していた物体が一定の加速度3.0m/s²で速さを増した。2.0秒後の物体の速さは何m/sか。

（2）1.0m/sの速さで運動していた物体が一定の加速度2.0m/s²で速さを増した。3.0秒後までに物体が進んだ距離は何mか。

（3）静止していた物体が動き出してから、2.0秒後に6.0m/sの速さになった。このときの加速度は何m/s²か。

（4）最初2.0m/sで運動していた物体が、3.0秒後には同じ向きに8.0m/sになった。このときの物体の加速度は何m/s²か。

（5）4.0m/sの速さで動いていた物体が、一定の加速度3.0m/s²で速さを増し、13m/sの速さになった。この間に物体が移動した距離は何mか。

（6）物体が移動しはじめてから3.0秒間に18m進んだ。このときの物体の加速度は何m/s²か。

練習問題　解答・解説

（1）8.0m/s

v0=2.0、a=3.0、Δt=2.0で、vを求めるので、
v=v0+atより
v=2.0+3.0×2.0=8.0

（2）12m

v0=1.0、a=2.0、Δt=3.0で、xを求めるので、
x=v0t+1/2at²より
x=1.0×3.0+1/2×2.0×3.0²＝12

（3）3.0m/s²

v0=0、Δt=2.0、v=6.0で、aを求めるので、
v=v0+atより
6.0=a×2.0
a=3.0

（4）2.0m/s²

v0=2.0、Δt=3.0、v=8.0で、aを求めるので、
v=v0+atより
8.0=2.0＋a×3.0
a=2.0

（5）27m

v0=4.0、a=3.0、v=13、t=不明で、xを求めるので、
v²－v0²=2axより
13²－4.0²=2×3.0×ｘ
x＝25.5
x≒26

（6）4.0m/s²

v0=0、t=3.0、x=18で、aを求めるので、
x=v0t+1/2at²より
18=1/2×a×3.0²
a=4.0