【物理基礎】力の合成・分解

物理基礎の力と運動の法則を学習します。今日は力の合成と分解です。中学校である程度学習は進んでいると思いますが、もう一度復習しておきましょう。

2力の合成

1つの物体にはたらく2つの力F₁、F₂からそれらを合わせたはたらきをする1つの力を求めることを力の合成といい、その1つの力を合力といいます。同一作用線上ではたらく2力は、向きをしっかりと確認し、以下のように合成します。

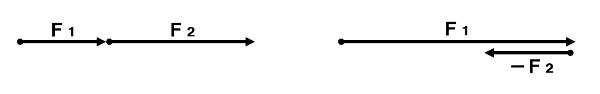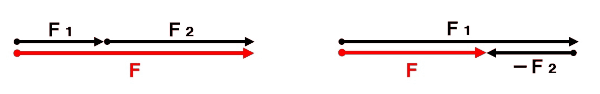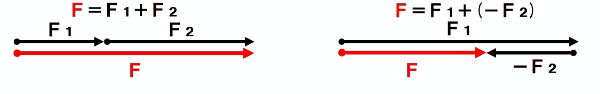
平行四辺形の法則

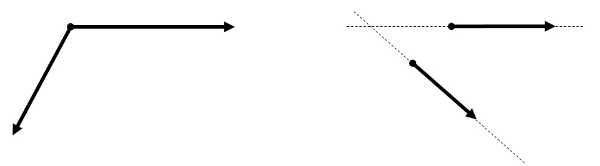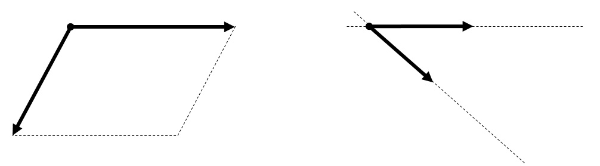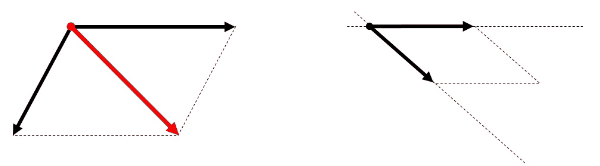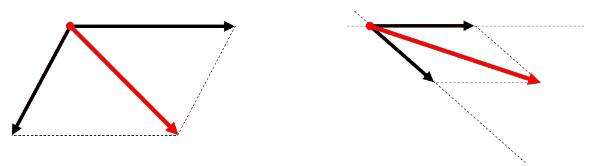
同一作用線上にない2力を合成する場合、力の大きさだけでなく、その向きも考慮する必要があります。向きを考えて力を合成する場合、平行四辺形の法則を利用します。また、力は作用線上を移動させることができるので、次の手順で作図を行います。

1. 2力の作用線の交点まで力の矢印を移動させる。
2. 力の矢印の先端を通り、もう一つの作用線に平行な補助線を2本引き、平行四辺形をつくる。
3. 平行四辺形の対角線を作用点から引く。

力の分解

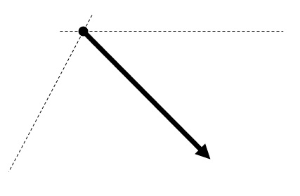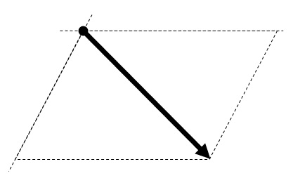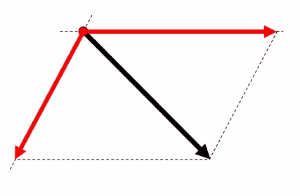
1つの力をそれと同じはたらきをする2つの力にわけることを力の分解といい、分解されてできた2力を、それぞれ分力といいます。力を分解するときも平行四辺形の法則を利用して作図します。

力の成分分け

大きさＦの力を、互いに直角に交わる2方向に分解したときの2つの分力を、Ｆの成分といいます。このとき、力を分解する2方向の一方をx方向、他方をy方向とすると、x方向の成分をＦx、y方向の成分をＦyと表します。

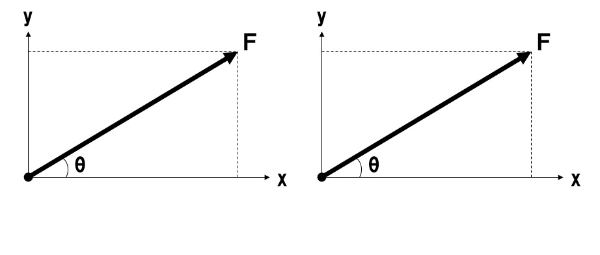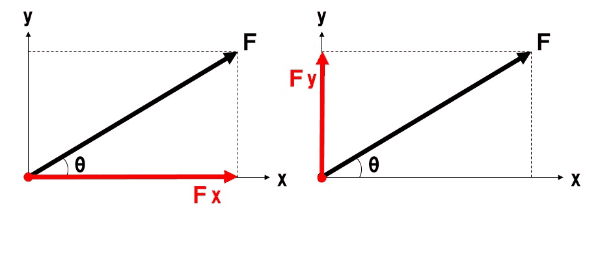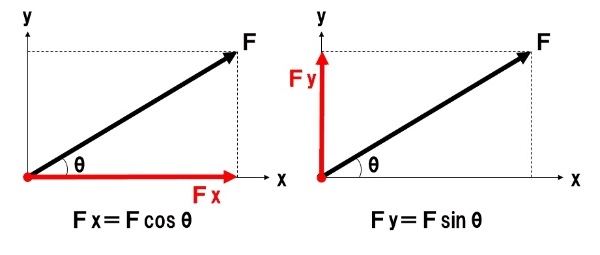
上図のように、x方向と力Ｆがなす角がθのとき、Ｆx、ＦyはＦ、θを用いて、

• Ｆx＝Ｆcosθ
• Ｆy＝Ｆsinθ

と表すことができます。

力の合成、分解、成分分けも、これから必ず必要になります。しっかりと作図できるように練習しておきましょう。