ニュートンの運動の第2法則である運動の法則。これは運動方程式という公式で表されます。その意味と使い方、さらに基本的な問題まで演習します。
運動方程式
運動方程式は、ニュートンの運動の法則を表したものです。運動の法則とは、超簡単にいうと「力を加えると、力の向きに加速するよ。」という法則です。次の運動方程式で表すことができます。
ma=F
m:質量[kg] a:加速度[m/s²] F:力(合力)[N]
力学台車に一定の大きさの力を加えると、等加速度運動を続けます。この加える力を2倍、3倍…と増やしていくと、力学台車の加速度の大きさは2倍、3倍…と増えていきます。したがって、加速度の大きさは加える力の大きさに比例することがわかります。
また、力の大きさを一定にしたままで、力学台車の質量を2倍、3倍…と増やしていくと、力学台車加速度の大きさは1/2倍、1/3倍…と減少します。したがって、加速度の大きさは質量に反比例することがわかります。
これを式で表したものが運動方程式ma=Fになるのです。
【練習問題】運動方程式の使い方
(1)2.0kgの物体に8.0Nの力をはたらかせると、生じる加速度は何m/s²か。
(2)5.0kgの物体に3.0m/s²の加速度を生じさせるには、何Nの力を加える必要があるか。
(3)100Nの力を加えると2.0m/s²の加速度を生じる物体の質量は何kgか。
(4)100gの物体に20cm/s²の加速度を生じさせる力の大きさは何Nか。
解答(1)4.0m/s² (2)15N (3)50kg (4)0.02N(2.0×10⁻²N)
運動方程式ma=Fに代入します。
(1)2.0×a=8.0 a=4.0
(2)5.0×3.0=F F=15
(3)m×2.0=100 m=50
(4)100gを0.1kg、20cm/s²を0.2m/s²に直して計算します。
0.1×0.2=F F=0.02
運動方程式の立て方
運動方程式を立てることで、物体にはたらく力の大きさや加速度を求めることができます。次の要領で式を立てていきましょう。水平な床で運動している場合。
- 運動方程式を立てようとする物体について、はたらく力(重力・接触力)をすべて矢印で図示する。
- 物体にはたらく力を運動方向(x方向)とそれに垂直な方向(y方向)に分解する。
- 運動方向(x方向)について、運動方程式をma=F(運動の向きを正とする)を立てる。
※物体が2物体あるときは、それぞれに運動方程式を立てる。 - 運動方向と垂直な方向(y方向)について、力のつり合いの式を立てる。
- それぞれの式を解いて、答えを求める。
実際に例題で確認しましょう。
【例題】運動方程式の立て方
なめらかな水平面上に質量5.0kgの物体を置き、水平に10Nの力を加え続けた。これについて、次の各問いに答えよ。
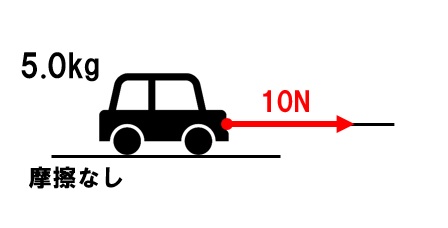
(1)物体の加速度の大きさは何m/s²か。
(2)動き始めてから5.0秒後の物体の速さは何m/sか。
解答(1)2.0m/s² (2)10m/s
(1)まずは、図にはたらいている力をすべて図示します。この問題の場合、重力mgと垂直抗力N、と運動の向きの力(10N)だけです。加速度も生じるのでaもかき入れます。
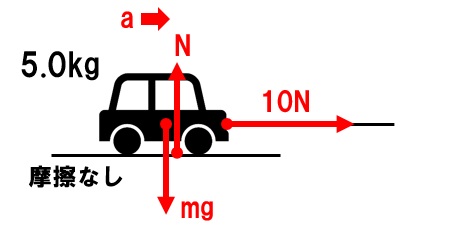
摩擦が無いので力がつり合っておらず、加速度が生じます。なので加速度が生じている方向を正の方向として運動方程式を立てます。
ma=Fに、m=5.0kg、F=10Nを代入
5.0×a=10
したがって、加速度の大きさは2.0m/s²になります。
垂直方向の力のつり合いの式は、今回必要ではないので書かなくてよいでしょう。
(2)加速度aがわかったので、等加速度直線運動の公式に代入して、5.0秒後の物体の速さを求めます。
v=v₀+atに、初速度v₀=0、加速度a=2.0、時間t=5.0を代入
v=0+2.0×5.0
したがって、5.0秒後の速さvは、10m/sだとわかります。

コメント