高1数学「高校数学Ⅰの1学期定期テスト対策問題」です。
【問題 高校数学Ⅰ】1学期定期テスト対策問題
【問1】整式の整理と加法・減法の問題

【問題DL】【1】整式の整理
【問2】乗法公式とその利用の問題

【問題DL】【2】乗法の公式とその利用
【問3】因数分解の問題
【3】次の因数分解をせよ。
(1)9x2+30xy+25y2
(2)3x2-10xy-8y2
(3)27x3+8y3
(4)x2+2xy+2x+6y-3
(5)2x2+xy-y2+x-5y-6
(6)x4-13x2+36
(7)x4+64
【問4】式の値の問題

(1)x+y
(2)xy
(3)x2+y2
(4)x3+y3
【問5】連立不等式の問題
次の(1)(2)の連立不等式を解け。(3)は問いに答えよ。

【問6】絶対値を含む方程式・不等式の問題
次の方程式、不等式を解きなさい。
(1)|x+4|=6
(2)|x+3|≦2
(3)|2x-3|>1
(4)3x-5=|x-3|
(5)|x+2|<2x
【問7】不等式の応用・文章題の問題
次の問いに答えなさい。
(1)1200円以内で、80円切手と50円切手を合わせて16枚買いたい。80円切手をできるだけ多く買うためには、それぞれ何枚買えばよいか、求めなさい。
(2)和が30である大小2つの数がある。小さい数を4倍すると大きい数よりも大きくなる時、小さい数の値の範囲を求めなさい。
(3)2つの容器A,Bがあって、Aには180cm3の水が、Bには80cm3の水が入っている。AとBから同じ量の水を汲み出し、Aの水の量がBの水の量の3倍以上5倍以下になるようにしたい。汲み出す水の量の範囲を求めよ。
【問8】2次方程式の解法の問題
次の2次方程式を解きなさい。
(1)x2+4x-2=0
(2)2x2-3x-1=0
(3)9x2-6x+1=0
(4)x2-18=0
(5)2x2-3x-1=0
(6)3x2-5x-2=0
【解答・解説 高校数学Ⅰ】1学期定期テスト対策問題
【問1】整式の整理と加法・減法のポイント・解答
- 整式は、xについて何次式かの問題は、xの最高次数を答える。
- xについての降べきの順の整理は、整式をxについて整理し、次数の高い方(大きい方)から順に並べる。
- 整式の加法・減法は、同類項どうしの和・差を計算する
- 定数や数と同じように考えている文字は定数という。
- 定数項は定数だけからなる項である。
【1】
(1)3次式
(2)x2の係数3 xの係数 定数項b
(3)3次式
(4)2次式
(5)2x2+(3y-5)x+(y2-4y+3)
【2】
(1)10x2+13x-1
(2)x2-11x+2
【問2】乗法公式のポイント:解答
高校生から新たに覚えるべき乗法の公式
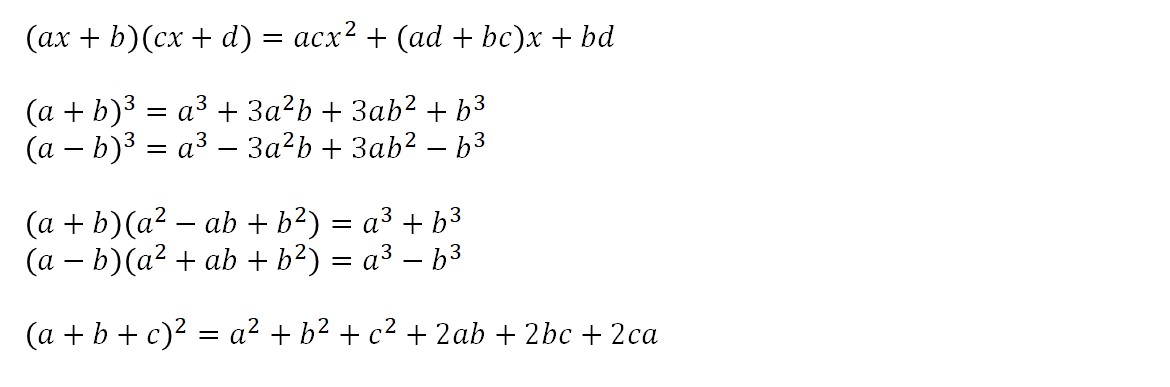
(1)9a10
(2)2x3+x2+5x+12
(3)6x2-5x-6
(4)8x3-36x2y+54xy2-27y3
(5)8x3-y3
(6)a4-4a3-19a2+46a+120
(7)a2+4b2+c2+4ab-4bc-2ca
【問3】因数分解のポイント・解答
因数分解は、展開の逆なので、「乗法公式の逆」を使うことも多い。
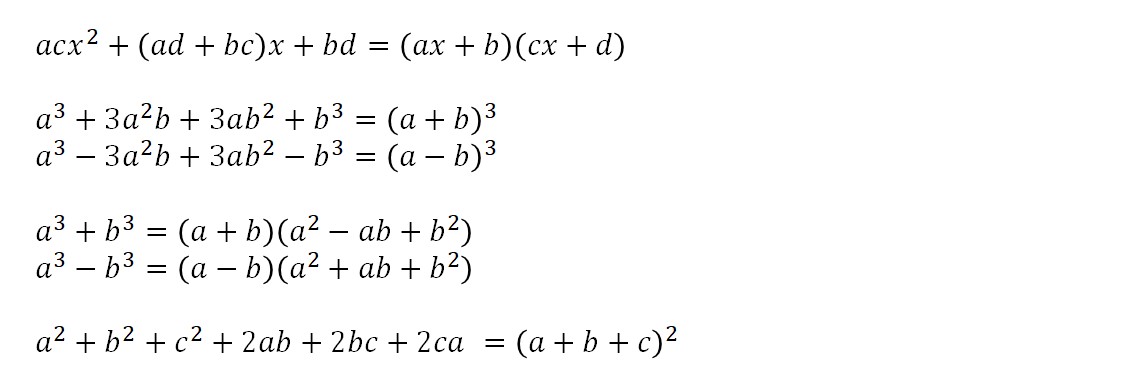
(1)(3x+5y)2
(2)(x-4y)(3x+2y)
(3)(3x+2y)(9x2-6xy+4y2)
(4)(x+3)(x+2y-1)
(5)(x+y+2)(2x-y-3)
(6)(x+2)(x-2)(x+3)(x-3)
(7)(x2+4x+8)(x2-4x+8)
【問4】式の値のポイント・解答
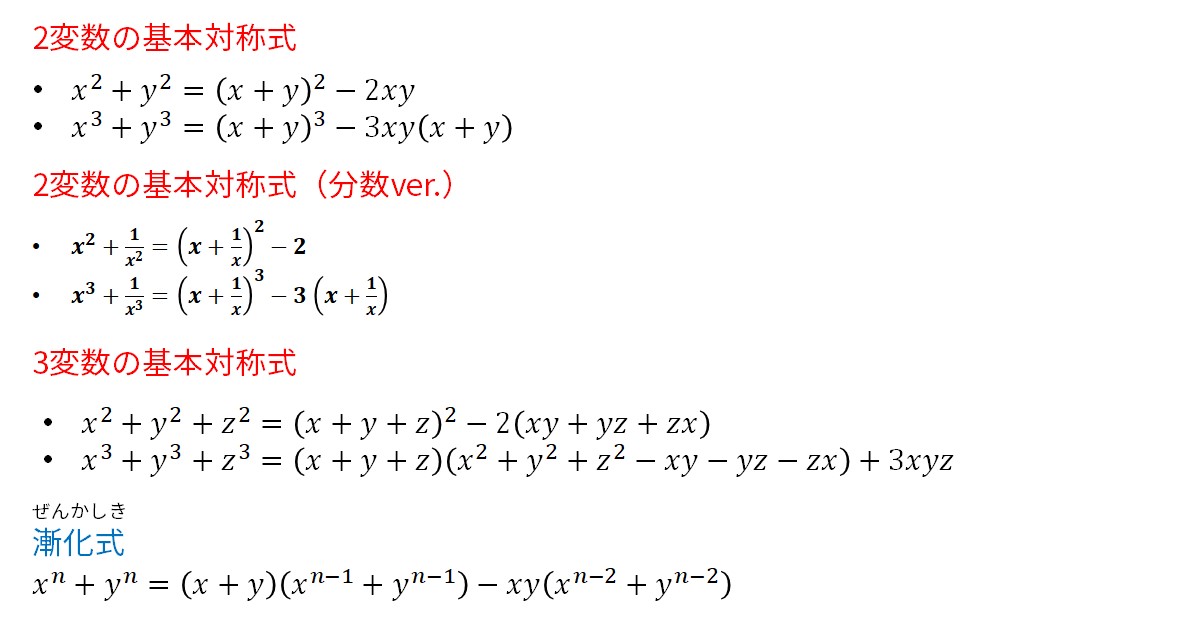

【問5】連立不等式の解説・解答
(1)の解説・解答
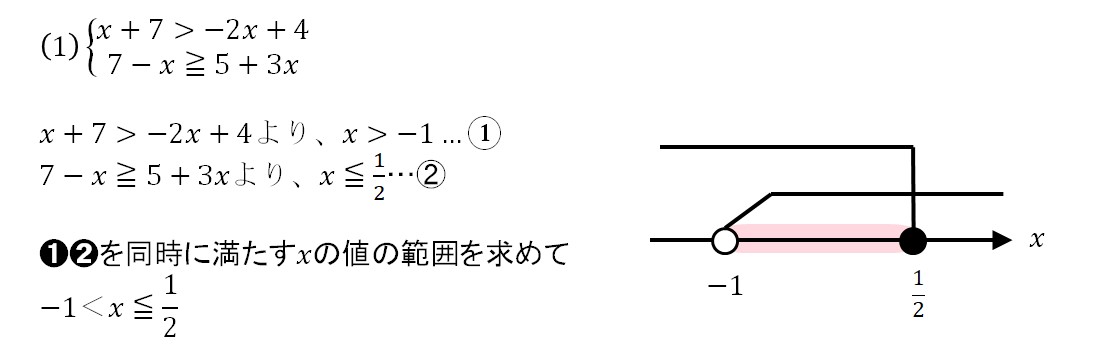
(2)の解説・解答

(3)の解説・解答
x=-1,2は解に含まれるから、この値を代入した不等式は成り立つ。
-2a<-3+a
4a<6+a
の連立不等式を解いて、
1<a<2
【問6】絶対値を含む方程式・不等式のポイント・解説
絶対値を含む方程式・不等式は、絶対値記号をはずしてから解きましょう。
<解法➊>
a≧0のとき、|a|=a
a<0のとき、|a|=-a
<解法➋>
※| |=数字の場合は、以下の性質を利用して解くことができる。
|a|=aの解は、x=±a
|a|<aの解は、-a<x<a
|a|>aの解は、x<-a、a<x
(ただし、a>0とする。)
(1)の解説
|x+4|=6より
x+4=±6
よって
x=2,-10
(2)の解説
|x+3|≦2より
-2≦x+3≦2
各辺から3を引いて
-5≦x≦-1
(3)の解説
|2x-3|>1より、
2x-3<-1、1<2x-3
よって、x<1,2<x
(4)の解説
3x-5=|x-3|
(ⅰ)x-3≧0つまり、x≧3のとき
3x-5=x-3
x=1
条件x≧3を満たさない。
(ⅱ)x-3<0つまり、x<3のとき
3x-5=-(x-3)
x=2
条件x<3を満たす
(ⅰ)(ⅱ)より方程式の解はx=2
(5)の解説
|x+2|<2x
(ⅰ)x≧2のとき
x+2<2x
x>2
条件を満たす。
(ⅱ)x<-2のとき
-(x+2)<2x
x>-2/3
条件を満たさない。
(ⅰ)(ⅱ)より方程式の解はx>2
【問7】不等式の応用・文章題の定期テスト対策問題の解説・解答
(1)の解説
80円切手をx枚買うとすると、
80x+50(16-x)≦1200
これを解くと
x=13.3…
よって、80円は13枚、50円は3枚
(2)の解説
小さい数をxとすると、大きい数は30-xとなる。
x<30-x<4x
これを解くと
6<x<15
(3)の解説
汲み出す水の量をxcm3とすると、題意より
3(80-x)≦180-x≦5(80-x)
3(80-x)≦180-xより、x≧30…①
180-x≦5(80-x)より、x≦55…②
①②より30≦x≦55
よって、汲み出す水の量は
30cm3以上55cm3以下である。
【問8】2次方程式の解法のポイント・解答
<2次方程式の解法の手順>
➊平方根の利用 x2=数字
➋因数分解の利用 ab=0ならばa=0またはb=0
➌平方完成 x2+偶数x+数字=0
➍解の公式(偶数ver.)

➎解の公式

(1)の解説

(2)の解説
左辺を因数分解すると
(2x-1)(x-1)=0
したがって2x-1=0 またはx-1=0
これを解くと
x=1/2 , 1
(※1/2は、2分の1)
(3)の解説
左辺を因数分解すると
(3x-1)2=0
したがって 3x-1=0
これを解くと
x=1/3
(※1/3は、3分の1)
(4)の解説
x2-18=0
x2=18
xは18の平方根だから
x=±3√2
(5)の解説
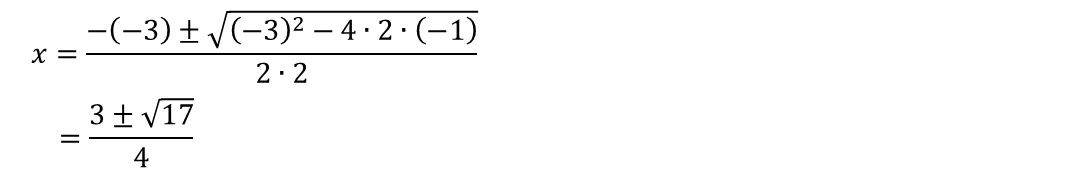
(6)の解説
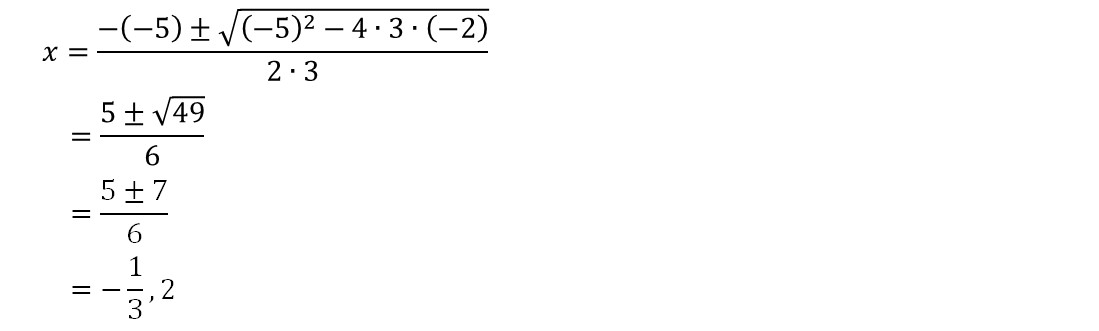

コメント